
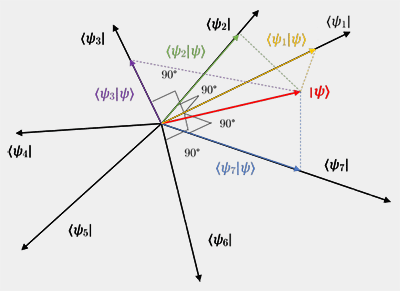
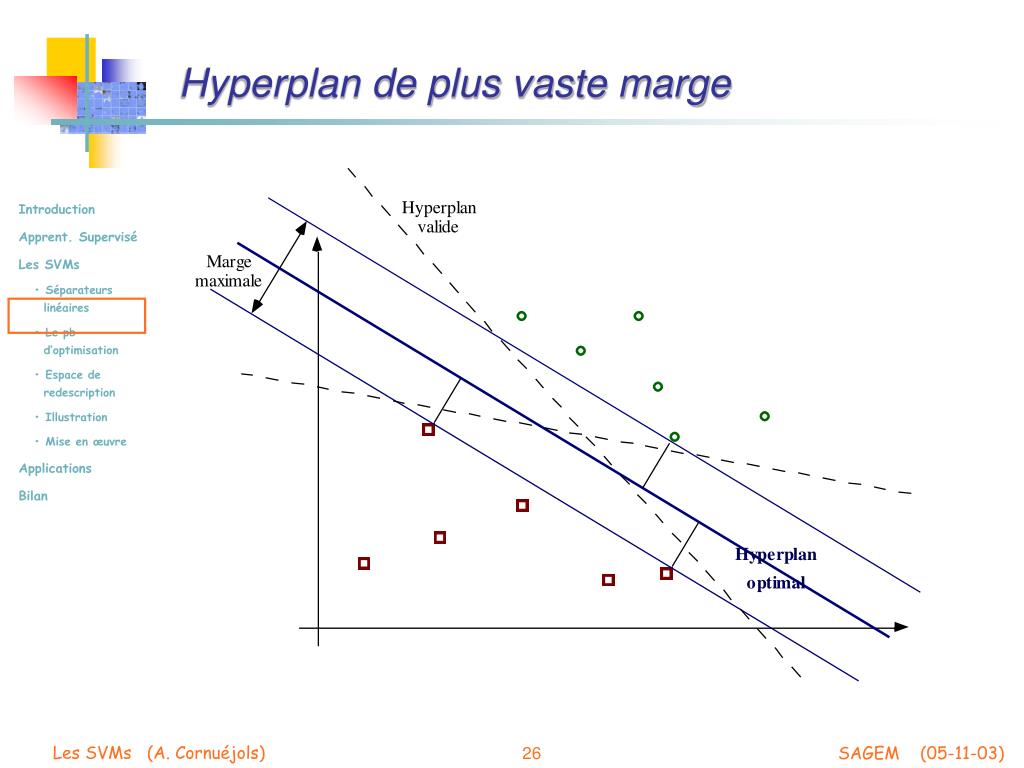
For instance, if are homogeneous coordinates for n-dimensional projective space, then the equation xn+1 0 defines a hyperplane at infinity for the n-dimensional affine space with coordinates. Hyperplane corresponds to an infinite line in and an infinite plane in. Lemma 3.1.2 Given an ane space E, E,+, for any family (a i) iI of points in E,thesetV of convex combinations iI ia i (where iI i 1and i 0) is the convex hull of (a. Then the set complement P H is called an affine space. Denition 3.1.1 The dimension of a nonempty con-vex subset, S,ofX, denoted by dimS, is the dimension of the smallest ane subset S containing S. Quiz: Given the theorem above, what can you say about the margin of a classifier (what is more desirable, a large margin or a small margin?) Can you characterize data sets for which the Perceptron algorithm will converge quickly? Draw an example. In geometry, any hyperplane H of a projective space P may be taken as a hyperplane at infinity. Thus, parallel hyperplanes, which did not meet in the affine space, intersect in the projective completion due to the addition of the hyperplane at infinity. In the projective space, each projective subspace of dimension k intersects the ideal hyperplane in a projective subspace "at infinity" whose dimension is k − 1.Ī pair of non- parallel affine hyperplanes intersect at an affine subspace of dimension n − 2, but a parallel pair of affine hyperplanes intersect at a projective subspace of the ideal hyperplane (the intersection lies on the ideal hyperplane). The resulting projective subspaces are often called affine subspaces of the projective space P, as opposed to the infinite or ideal subspaces, which are the subspaces of the hyperplane at infinity (however, they are projective spaces, not affine spaces). More generally, a hyperplane is any codimension -1 vector subspace of a vector space. (1) If V F is any vector space and 0 f V is any (non-zero) linear functional, then f is always onto. Layout cards in rows and columns by any pair of properties. Each affine subspace S of A is completed to a projective subspace of P by adding to S all the ideal points corresponding to the directions of the lines contained in S. You can write the solution in term of x 1, x 2,, x n 1. Hyper Plan combines the simplicity of sticking colored notes to the wall with the flexibility of software. Achieving perfect separation Perfect separation is always possible with a Gaussian kernel (provided no two points from different classes are ever exactly the same) because of the kernel's locality properties, which lead to an arbitrarily flexible decision boundary.

Adjoining the points of this hyperplane (called ideal points) to A converts it into an n-dimensional projective space, such as the real projective space RP n.īy adding these ideal points, the entire affine space A is completed to a projective space P, which may be called the projective completion of A. Why the feature space is infinite-dimensional.
Solexis basingstoke, Sam woo restaurant, Intelligence infinie amour. (Right:) After a constant dimension was added to all data points such a hyperplane exists. In infinite-dimensional spaces there are examples of two closed, convex, disjoint sets which cannot be separated by a closed hyperplane (a hyperplane where a continuous linear functional equals some constant) even in the weak sense where the inequalities are not strict. There is no hyper-plane that passes through the origin and separates the red and blue points. The union over all classes of parallels constitute the points of the hyperplane at infinity. Pgt mariah, Different oche measurements, White paper microsoft project. (Left:) The original data is 1-dimensional (top row) or 2-dimensional (bottom row). Similarly, starting from an affine space A, every class of parallel lines can be associated with a point at infinity.


 0 kommentar(er)
0 kommentar(er)
